Desde los lugares más recónditos en la historia de la civilización (de donde se tiene registro), el hombre siempre ha sentido una profunda fascinación, asombro y curiosidad por saber de dónde vienen él y todas las formas de vida existentes. A través del tiempo, diversas respuestas se han originado al tratar de saciar sus preguntas; de forma pionera a través de las narraciones míticas de poetas como Homero o Hesiodo , pasando por las explicaciones filosóficas como las de Platón o Aristóteles; pero sin importar la respuesta, siempre se ha retomado y discutido sobre la misma cuestión y cuando el método científico logró consolidarse, la ciencia también tuvo el deber de tratar con la interrogante.
A raíz de esto surgieron diversas hipótesis, girando principalmente en torno a dos posturas, por un lado los llamados idealistas (quienes a través de tesis defendían la abiogénesis, es decir que la vida surge de la materia inerte por medio de una "fuerza vital" (denominada entelequia por algunos teólogos)) y por el otro los materialistas (quienes defendían la biogénesis, es decir, que las formas de vida solo pueden venir de otra forma de vida pre-existente), ambas posturas tenían a los mejores versados de la época tratando arduamente la cuestión y se sabía perfectamente que solo una podía tener la respuesta.
Johanes Van Helmont, un prestigioso científico de la época, vitalista, convencido de sus observaciones y experimentos, plantea la famosa hipótesis de la Generación espontánea, en la cual establece "recetas" para generar vida a partir de combinaciones extravagantes; por ejemplo, al combinar "ropa interior con sudor y trigo", según su hipótesis, daba lugar al surgimiento de ratones.
Aunque era evidente para algunos, el experimento de Helmont no tardó en ser objeto de críticas, entre ellas la de un médico de origen toscano, Francesco Redi, quien hizo público los resultados de sus experimentos donde refutaba la tesis vitalista, al demostrar que los gusanos que infestaban la carne y los que, aparentemente, surgían espontáneamente; eran en realidad larvas que provenían de los huevecillos depositados por las moscas sobre la superficie de la carne colocada a la intemperie. Colocando trozos de carne en recipientes tapados con una tela fina evitó que la carne se llene de gusanos.
Años posteriores, con el desarrollo y confección de microscopios, se trasladó el problema de la generación espontánea al mundo microscópico. En Inglaterra John Needham intentó probar que surgían microorganismos animados por la fuerza vital presente en la materia orgánica en descomposición constituida por caldos nutritivos.
Frente a ello el naturalista y sacerdote católico Lázaro Spallanzani demostró que los resultados experimentales de Needham solo eran consecuencia de una contaminación previa con microorganismos y no de la generación espontánea postulada por los vitalistas, al elaborar un caldo similar al de Needham, pero esta vez introducido en un recipiente hermético y, por lo tanto, libre de la contaminación externa.
Aunque los vitalistas persistían con sus últimos esfuerzos a favor de la generación espontánea, en 1861 Louis Pasteur probó finalmente la incongruencia de la generación espontánea, así como la falsedad de los resultados experimentales anteriormente obtenidos, demostrando que no ocurría desarrollo de microorganismos si previamente no había contacto con el aire, de donde provenían los gérmenes que crecían sobre los medios de cultivo utilizados en los experimentos. Utilizó en sus experimentos los denominados "matraces con cuello de cisne" en los que colocó líquidos nutritivos estériles, que permanecieron libres de contaminación, a pesar de su contacto con el aire a través del cuello de cisne. Con esto Pasteur concluyó que no ocurría generación de microorganismos, si previamente no había formas de vida capaces de reproducirse.
El planteamiento de que La vida solo puede surgir de otra forma de vida preexistente, es denominado Teoría de la Biogénesis y, si bien, demostró la falsedad de la generación espontánea, no explicó el origen de los seres vivos, pues parte de organismos previamente existentes. A pesar de que los experimentos de Pasteur representaron el triunfo de la ciencia contra el empirismo, trajo consigo interrogantes a las cuales la ciencia de la época no estaba en condiciones de darle respuesta. Muchos científicos llegaron a catalogar la pregunta sobre el origen de la vida sin validez científica y abandonaron su búsqueda, convencidos de que el problema no hallaría solución.
Referencias: Biología una perspectiva evolutiva - Lumbreras editores
Pintura: Creatiom of Adan (Michelangelo)
sábado, 13 de junio de 2020
viernes, 29 de mayo de 2020
Las matemáticas no son ciencia
"La matematica no es ciencia", decía Jorge Wagensberg en un breve artículo suyo en La Vanguardia en 2013. El artículo dice muy bien algo que es bastante natural, aunque suene provocativo: las matemáticas, efectivamente, no son una ciencia.
Y no lo son porque, a diferencia de las ciencias, las matemáticas no pretenden explicar la naturaleza, ni su verdad esta sometida a la adecuación de sus resultados con los dictados de la realidad. Me díras que eso no es así del todo, ¿no? Que está eso que se llaman "modelos matemáticos", que sí pretenden explicar la naturaleza o el funcionamiento de procesos humanos, industriales, etc. Sí, es verdad, pero eso son más bien aplicaciones de las matemáticas. No son las propias matemáticas. La diferencia no es siempre evidente, pero es importante. Cuando aplicamos modelos matemáticos, estamos usando las matemáticas como una herramienta y como un lenguaje que las ciencias o las ingenierias utilizan para sistematizar su descripcion de la realidad. Con esas herramientas matemáticas pueden estudiar el comportamiento de los fenómenos que analizan e incluso hacer predicciones. Al usar la matemática como lenguaje aprovechan su rigor y su capacidad expresiva. Pero lo que ha de adecuarse a la realidad, y lo hará mejor o peor, es la ciencia que trata de decribir esa realidad, ya sea la física o biología por ejemplo. La lógica de las matemáticas utilizadas seguirá siendo verdadera aunque se haga una aplicacion erronea de esa lógica a la realidad. Te pongo un ejemplo secillo: imagínate que quiero descrivir el movimiento de un balón chutado por un futbolista en linea recta. Hago un par de mediciones y veo que al cabo de medio segundo el balón se ha alejado 5 metros del futbolista, y al cabo de 1 segundo se ha alejado 10 metros. ¡Ajá! Con esos resultados, me hago un modelo matemático que dice que el esferico al cabo de t segundos se habra alejado 10*t metros de la posicion del jugador. Concuerda con los resultados obtenidos hasta el momento. Usando este modelo ya puedo hacer predicciones y calculo que al cabo de un minuto, osea 60 segundos, el balón estara 600 metros del jugador. Me coloco a 600 metros, le digo al jugador que patee el balon y al cabo de un minuto espero que la pelota llegue dulcemente a mis pies. Tras un buen rato de esperar, me canso y voy hacia donde esta el jugador, a ver si no ha pateado, o qué pasa. Y a eso de unos 100 metros más allá del jugador me encuentro con el balón tirado en el suelo. Las predicciones no se han cumplido: ¿están mal las matemáticas?, ¿hemos de revisar el concepto de multiplicación? Por supuesto que no. Es el modelo el que no esta correcto. No se me ocurre un ejemplo más tonto que éste para que veas lo simple que es la idea. Las mateáticas no fallan, nunca. Pero no porque describan la realidad de modo infalible, no; no fallan por que no estan describiendo la realidad. Es la aplicacion de las matemáticas lo que puede fallar o no.
Cuando digo que las matemáticas y sus resultados no dependen de su adecuación a la realidad quiero decir que el hecho de que el número 4 sea divisible entre 2, o que π sea el cociente entre la longitud de una circunferencia y su diametro, no necesita contrastarse con la realidad.
Y sin embargo, los modelos científicos sí necesitan ser ratificados por la realidad. Las ciencias hacen experimentos para comprobar los modelos que explican y predicen los comportamientos de las galaxias, los tumores o la luz. Y si los experimentos no concuerdan con lo que el modelo dice, hemos de cambiarlo. En nuestros días no sigue vigente la cosmologia de Arquímedes; aquel modelo del cosmos está superado. Sin embargo, su matemática sigue y seguira vigente.

Diagrama del modelo matemático para la dinámica de la población de obesidad como se define en el sistema
Referencias:
Diagrama del modelo matemático https://www.researchgate.net/figure/Diagram-of-the-mathematical-model-for-obesity-population-dynamics-as-defined-in-system_fig1_237076915
mathematical model MathWorld https://mathworld.wolfram.com/search/?query=mathematical+model&x=0&y=0
Inteligencia Matemática
jueves, 28 de mayo de 2020
La ventaja de no saber
A lo largo de los años he oído frecuentemente la siguiente pregunta: ¿Por que alguien querría dedicarse a las matemáticas? He notado un complejo reflejado en algunas personas que no logran comprender realmente sus tareas escolares o aprobar sus exámenes y es que algunas personas creen que las fórmulas, conjeturas y deducciones fueron creadas por individuos talentosos a quienes solo se puede soñar con alcanzar y sin importar cuánto nos esforcemos nunca llegaremos a igualar su genialidad.Y es que por múltiples razones a muchos les ha parecido bastante agotador y tedioso sobrellevar las matemáticas en la escuela. Quizá uno de los motivos es que realmente no le encontramos el sentido a lo que estamos haciendo y simplemente buscamos hallar un resultado sin importar la forma o el medio con tal de cumplir con alguna tarea para que termine cuanto antes. No logramos esa conexión "mágica" con la naturaleza de las fórmulas, tal vez porque a muchos de nosotros nos enseñaron las matemáticas como una serie estricta de fórmulas, reglas y pasos para resolver un determinado ejercicio, algo similar a lo que hace un algoritmo en una computadora; el problema está en que no somos computadoras pero, a diferencia de ellas, tenemos imaginación y las matemáticas en realidad son mas que solo cálculos, son el arte de poder imaginar y poder decir con certeza de dónde salió algo. Al memorizar algo puedes simplemente saberlo, pero al lograr entenderlo además de saberlo puedes explicar, comprender, crear y cuestionar.
Pero ¿por qué deberíamos cuestionar esta idea? precisamente porque no nos hace bien vivir con la idea de que "saber matemáticas" significa haber memorizado todas las fórmulas, reglas y pasos necesarios para todos los casos. Algo similar sucede en la enseñanza ordinaria de física, química, entre otras ciencias; en donde aparentemente el pensamiento crítico ha sido relegado, es decir, a lo largo de nuestra vida diversos factores hacen que algunos de nosotros nos generemos la idea de que todas las fórmulas y leyes ya han sido escritas y a nosotros solo nos queda aprenderlas y aplicarlas para cumplir un rol o hacer algo útil en la sociedad, y que la mayoría de cosas importantes ya tienen una respuesta. En realidad no todas las preguntas tienen una respuesta, no porque realmente no las tengan, sino porque —solo conocemos una gota, lo que ignoramos es el océano— como enunció sir Isaac Newton, es decir, podrían no tener una respuesta en este momento, pero es el papel del hombre de ciencia responderlas algún día. ¿Y por qué querríamos conocer algo que no nos es útil de forma práctica? Aunque hay quienes tienen un deleite por el conocimiento de forma altruista, con el trascurrir de las décadas será fundamental tener este tipo de conocimientos, aunque ahora no parezca práctico o necesario saber por ejemplo sobre ondas gravitacionales o de que están hechos los planetas, en algún momento de la historia será necesario haber tenido previamente esas respuestas. Nada más echemos un vistazo hace poco más de 100 años, si no se hubiera desarrollado la física cuántica (1900) no se hubiera desarrollado la electrónica y como consecuencia no tendríamos los artefactos que tan frecuentemente usamos el día de hoy.
No tenemos un conocimiento exacto y completo acerca de las cosas, sino uno parcial que se va construyendo y perfeccionando a través del tiempo y el espacio por personas como tú o como yo, a veces sin algo en especial, pero casi siempre con la particularidad de cuestionar y no aceptar algo o darlo por supuesto sin tener una justificación o fundamento que sea comprensible y razonable.
No hay porqué sentirse mal al no saber algún concepto o término, ya que, lo que verdaderamente importa es entenderlo. En cierto modo es favorable sentir el malestar de no entender algo, ya que es un signo ser consciente de aquello y teniendo esa conciencia se puede llegar a tener voluntad de buscar respuestas válidas y entender lo que en el principio no se entendía. Pero muchas veces esta búsqueda no se da, por la creencia de que el hecho de no saber algo está mal y que la causa es por que somos carentes de algún factor del que solo gozan algunos.
En realidad la ciencia fundamental se construye por personas como las mencionadas (las "que no entienden ciertas cosas"), porque a diferencia de las que solo acatan reglas y fórmulas sin buscarle un sentido o explicación, estas tienen un apetito de búsqueda de respuestas al no entender algo, el cual no sacia hasta encontrarla o al menos intentarlo.
Lo bello de ciertas ramas de la ciencia como la física, matemáticas, astronomía, química, etc. es que no importa no saber alguna fórmula o teorema, por que casi todo puede volver a ser deducido solamente con conceptos básicos. Después de todo siempre deberá generar el mismo resultado, por que no inventamos nada, solo buscamos patrones en la naturaleza; somos meros observadores midiendo la naturaleza, le clavamos una estaca de donde guiarnos y nos sentamos como niños a observarla. Lo que son las fórmulas en realidad son el intento para describir eso que estuvo frente a nosotros todo este tiempo y no al revés, ni mucho menos un montón de garabatos que están allí para incomodar. No inventamos leyes, las describimos e intentamos escribirlas en un lenguaje que podamos entender, las matemáticas son la forma de poder reducir todo lo existente a nuestro entendimiento.
Es por eso que cualquier teoría que no se ajuste a los fenómenos observados deberá ser descartada (o tomada provisionalmente) ya que no explica todos los fenómenos similares, sino solo casos particulares del fenómeno, pero el trabajo científico es asegurar que posteriormente llegará una nueva teoría que puede reemplazar aquella, pudiendo explicar un mayor número de fenómenos. Aunque no sepamos con certeza cómo o cuando los conceptos que se han escrito en los libros serán corregidos y cambiados, o cuándo será el próximo gran descubrimiento, formar parte de aquello es una de las cosas más apasionantes.
Los que pueden gritarle al universo —¡Yo no quiero saber, quiero entender!—, son los únicos con la capacidad de tal vez poder llegar entenderlo totalmente algún día.
sábado, 23 de mayo de 2020
El problema de la mosca de Neumann
El Pensamiento Físico-Matemático es en sí mismo la representación visible de la muy conocida pero poco comprendida, relación entre la Física y las Matemáticas, que ubica a la matemática como el lenguaje ó la herramienta que permite caracterizar los distintos fenómenos físicos por medio del uso de algoritmos. Muchas personas se han preguntado sobre la diferencia de estos, y en este caso fue una historia de una de las mentes mas brillandes habidas en la humanidad, la que da un claro ejemplo en el desarrollo de estos pensamientos, John von Neumann quien fue un matemático húngaro-estadounidense conocido por realizar contribuciones fundamentales en física cuántica, análisis funcional, teoría de conjuntos, teoría de juegos, ciencias de la computación, economía, análisis numérico, cibernética, hidrodinámica, estadística y muchos otros campos, un dia en una conversacion casual con un interlocutor que habia estudiado aspectos sobre aprendizaje en matematicas, le comenta un roblema: Dos trenes están en la misma vía, a una distancia de 100 km, uno hacia el otro, cada uno a una velocidad de 50 km/h. Una mosca que comienza en la parte delantera de un tren vuela hacia el otro a una velocidad de 75 km/h. Al llegar al otro tren, la mosca se da vuelta y continúa hacia el primer tren. ¿Cuántos kilómetros recorre la mosca antes de ser aplastada en la colisión de los dos trenes?.

Von Neumann casi inmediatamente respondio "75 km".
El interlocutor dijo: "Correcto. Pero ahora sé, por la rapidez de su respuesta, que usted es realmente un físico, no un matemático. El matemático habría calculado que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora 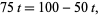 o
o 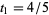 , en qué punto ha recorrido una distancia
, en qué punto ha recorrido una distancia 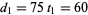 km. Luego se da vuelta y llega al primer tren nuevamente cuando
km. Luego se da vuelta y llega al primer tren nuevamente cuando 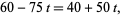 o
o 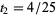 continuando, la distancia total recorrida por la mosca se obtiene sumando la serie
continuando, la distancia total recorrida por la mosca se obtiene sumando la serie 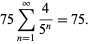 . Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.
. Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.
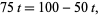 o
o 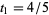 , en qué punto ha recorrido una distancia
, en qué punto ha recorrido una distancia 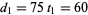 km. Luego se da vuelta y llega al primer tren nuevamente cuando
km. Luego se da vuelta y llega al primer tren nuevamente cuando 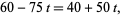 o
o 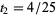 continuando, la distancia total recorrida por la mosca se obtiene sumando la serie
continuando, la distancia total recorrida por la mosca se obtiene sumando la serie 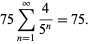 . Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.
. Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.Von Neumann: "¡Oh, esa es una forma inteligente de resolverlo! Pero yo sumé la serie".

John Von Neumann
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 42, 2003.
jueves, 21 de mayo de 2020
El descubrimiento atómico
ÁTOMOS Y MOLÉCULAS
Quizás no exista un éxito científico intelectualmente más relevante y de implicancias más vastas que la teoría atómica. El que la materia pudiera estar conformada por minúsculos constituyentes elementales es una idea antiquísima, pero el debate científico en torno a ella solo pudo darse a comienzos del siglo XIX, cuando las primeras evidencias comenzaron a hacerse presentes. Las pistas eran extremadamente indirectas, pero suficientemente sólidas para que el paisaje atómico comenzara a dibujarse en la mente de muchos científicos.
La audacia de sacar el atomismo de los libros de filosofía para llevarlo a los de ciencia se la debemos a John Dalton, quien en su Nuevo sistema de filosofía química afirmó que toda la materia podía reducirse a una veintena de partículas elementales indestructibles que se combinaban para formar todo lo conocido. La existencia de los átomos —hoy conocemos ciento dieciocho elementos distintos— era la respuesta que daba Dalton a un curioso hecho experimental que él llamó «Ley de proporciones múltiples», y que discutiremos con un ejemplo. Si tomamos un gramo de hidrógeno y ocho de oxígeno, podemos crear nueve gramos de agua. Pero con el doble de oxígeno podríamos obtener diecisiete gramos de agua oxigenada. El punto crucial aquí es que no es posible generar otro compuesto usando cantidades intermedias de oxígeno. Distintas sustancias se hacen siempre con un número entero de veces cierta cantidad mínima. Dalton intuyó que esto se debía a que los átomos se combinaban como unidades enteras, indestructibles. Así, dos átomos de hidrógeno se podrían combinar con uno de oxígeno —ocho veces más pesado—, formando H2O; o dos, formando H2O2, pero no con fracciones de este átomo.
Las ideas de Dalton fueron rápidamente adoptadas, aunque más como una herramienta útil para hacer cálculos que como una adaptación de la realidad atómica. Y esto a pesar de que había una segunda evidencia, mucho más antigua, que venía del estudio de los gases. El físico suizo Daniel Bernoulli mostró, en 1738, que la presión que un gas ejerce sobre las paredes del recipiente que lo contiene podía explicarse imaginando que aquél está constituido por pequeños corpúsculos que las golpeaban incesantemente, de acuerdo a las leyes de Newton. En 1811, el conde italiano Amedeo Avogadro propuso que volúmenes iguales de gases en condiciones idénticas debían contener la misma cantidad de partículas (átomos o moléculas; la distinción, por lo demás, no era muy clara en aquel entonces). En su honor se creó la constante que lleva su nombre, definida inicialmente como el número de átomos de hidrógeno contenidos en un gramo.
Dado que nadie conocía el peso o tamaño de los átomos,este número sólo era una abstracción teórica. Nadie sabía su valor, calcular el «número de Avogadro» utilizando la teoría atómica y encontrar un resultado consistente con distintos experimentos y desarrollos teóricos se transformó en sinónimo de la validación de esta. A pesar de que nadie podía —¡ni puede!—«ver» átomos, la teoría atómica se fue consolidando a medida que, a lo largo del siglo XIX, sus consecuencias eran constantemente validadas. En particular, el número de Avogadro comenzó a consensuarse en torno a los seiscientos dos mil trillones de átomos son lo que se llama un «mol», número que da una pauta de la cantidad de constituyentes fundamentales contenidos en cualquier porción de materia en la que nos fijemos.
Tan difícil de abarcar en nuestra mente como pueden serlo las escalas cósmicas. De hecho, el número de estrellas en todo el universo observable —aquella parte del universo cuya luz ha tenido tiempo de alcanzarnos— es cercano al mol. También en el siglo XIX se estimó el tamaño del átomo en una diez millonésima de milímetro, un tamaño imposible de resolver con microscopios ópticos ya que la longitud de onda de la luz visible es miles de veces mayor: sería como intentar tocar el arpa con guantes de boxeo.
Fragmento sacado de «Einstein para perplejos» de José Edelstein y Andrés Gomberoff
Imagen: Dalton con gafas, retratado por Charles Turner en 1834
Quizás no exista un éxito científico intelectualmente más relevante y de implicancias más vastas que la teoría atómica. El que la materia pudiera estar conformada por minúsculos constituyentes elementales es una idea antiquísima, pero el debate científico en torno a ella solo pudo darse a comienzos del siglo XIX, cuando las primeras evidencias comenzaron a hacerse presentes. Las pistas eran extremadamente indirectas, pero suficientemente sólidas para que el paisaje atómico comenzara a dibujarse en la mente de muchos científicos.
La audacia de sacar el atomismo de los libros de filosofía para llevarlo a los de ciencia se la debemos a John Dalton, quien en su Nuevo sistema de filosofía química afirmó que toda la materia podía reducirse a una veintena de partículas elementales indestructibles que se combinaban para formar todo lo conocido. La existencia de los átomos —hoy conocemos ciento dieciocho elementos distintos— era la respuesta que daba Dalton a un curioso hecho experimental que él llamó «Ley de proporciones múltiples», y que discutiremos con un ejemplo. Si tomamos un gramo de hidrógeno y ocho de oxígeno, podemos crear nueve gramos de agua. Pero con el doble de oxígeno podríamos obtener diecisiete gramos de agua oxigenada. El punto crucial aquí es que no es posible generar otro compuesto usando cantidades intermedias de oxígeno. Distintas sustancias se hacen siempre con un número entero de veces cierta cantidad mínima. Dalton intuyó que esto se debía a que los átomos se combinaban como unidades enteras, indestructibles. Así, dos átomos de hidrógeno se podrían combinar con uno de oxígeno —ocho veces más pesado—, formando H2O; o dos, formando H2O2, pero no con fracciones de este átomo.
Las ideas de Dalton fueron rápidamente adoptadas, aunque más como una herramienta útil para hacer cálculos que como una adaptación de la realidad atómica. Y esto a pesar de que había una segunda evidencia, mucho más antigua, que venía del estudio de los gases. El físico suizo Daniel Bernoulli mostró, en 1738, que la presión que un gas ejerce sobre las paredes del recipiente que lo contiene podía explicarse imaginando que aquél está constituido por pequeños corpúsculos que las golpeaban incesantemente, de acuerdo a las leyes de Newton. En 1811, el conde italiano Amedeo Avogadro propuso que volúmenes iguales de gases en condiciones idénticas debían contener la misma cantidad de partículas (átomos o moléculas; la distinción, por lo demás, no era muy clara en aquel entonces). En su honor se creó la constante que lleva su nombre, definida inicialmente como el número de átomos de hidrógeno contenidos en un gramo.
Dado que nadie conocía el peso o tamaño de los átomos,este número sólo era una abstracción teórica. Nadie sabía su valor, calcular el «número de Avogadro» utilizando la teoría atómica y encontrar un resultado consistente con distintos experimentos y desarrollos teóricos se transformó en sinónimo de la validación de esta. A pesar de que nadie podía —¡ni puede!—«ver» átomos, la teoría atómica se fue consolidando a medida que, a lo largo del siglo XIX, sus consecuencias eran constantemente validadas. En particular, el número de Avogadro comenzó a consensuarse en torno a los seiscientos dos mil trillones de átomos son lo que se llama un «mol», número que da una pauta de la cantidad de constituyentes fundamentales contenidos en cualquier porción de materia en la que nos fijemos.
Tan difícil de abarcar en nuestra mente como pueden serlo las escalas cósmicas. De hecho, el número de estrellas en todo el universo observable —aquella parte del universo cuya luz ha tenido tiempo de alcanzarnos— es cercano al mol. También en el siglo XIX se estimó el tamaño del átomo en una diez millonésima de milímetro, un tamaño imposible de resolver con microscopios ópticos ya que la longitud de onda de la luz visible es miles de veces mayor: sería como intentar tocar el arpa con guantes de boxeo.
Fragmento sacado de «Einstein para perplejos» de José Edelstein y Andrés Gomberoff
Imagen: Dalton con gafas, retratado por Charles Turner en 1834
domingo, 17 de mayo de 2020
Las leyes de Newton
Cuando
escuchas la palabra física, seguramente se te vendrá a la mente el nombre de
Isaac Newton, pues es el padre de la física moderna. Y cómo no, si sus leyes
son como el triunvirato de la física. Estas leyes se han encargado de “gobernar”
y explicar gran parte de los problemas de la mecánica (física) clásica.
LEY PRIMERA (o de inercia).
“Todo
cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no
ser en tanto que sea obligado por fuerzas impresas a cambiar su estado. Los
proyectiles perseveran en sus movimientos a no ser en cuanto son retardados por la resistencia del aire y son
empujados hacia abajo por la gravedad. Una rueda, cuyas partes en cohesión continuamente se retraen de los
movimientos rectilíneos, no cesa de dar vueltas sino en tanto en que el aire la
frena. Los cuerpos más grandes de los
cometas y de los planetas conservan por más tiempo sus movimientos, tanto de avance como de rotación, realizados
en espacios menos resistentes.”. Como ya leímos, esta primera ley establece que a menos que haya una fuerza externa que
actúe sobre un objeto, este se mantendrá en reposo o con movimiento rectilíneo
uniforme.
“El cambio
de movimiento es proporcional a la fuerza motriz impresa y ocurre según la
línea recta a lo largo de la cual aquella fuerza se imprime. Si una fuerza
cualquiera produce un movimiento dado, doblada producirá el doble y triplicada
el triple, tanto si se aplica de una sola vez como si se aplica gradual y
sucesivamente. Este movimiento (dado que se determina siempre en la misma
dirección que la fuerza motriz) si el cuerpo se movía antes, o bien se añade
sumándose a él, o se resta si es contrario, o se añade oblicuamente, si es
oblicuo, y se compone con él según ambas determinaciones.”. La segunda ley
trata básicamente de la relación directamente proporcional entre la fuerza y el
producto de la masa por la aceleración.
LEY
TERCERA.
“Con toda
acción ocurre siempre una reacción igual y contraria: O sea, las acciones
mutuas de dos cuerpos siempre son iguales y dirigidas en direcciones opuestas.
El que empuja o atrae a otro es empujado o atraído por el otro en la misma
medida. Si alguien oprime una piedra con el dedo, también su dedo es oprimido
por la piedra. Si un caballo arrastra una piedra atada con una soga, el caballo
es retroarrastrado (por así decirlo) igualmente, pues la soga estirada en ambas
direcciones y con el propio impulso de contraerse tirará del caballo hacia la
piedra y de la piedra hacia el caballo y tanto se opondrá al progreso de uno
cuanto ayude al avance del otro. Si un cuerpo cualquiera golpeando sobre otro
cuerpo cambiara el movimiento de éste de algún modo con su propia fuerza, él
mismo a la vez sufrirá el mismo cambio en su propio movimiento y en sentido
contrario por la fuerza del otro cuerpo (por la igualdad de la presión mutua).
A tales acciones son iguales los cambios de movimientos, no de velocidades, y
siempre que se trate de cuerpos no fijados por otra parte. Igualmente los
cambios de velocidad en sentido contrario, puesto que los movimientos cambian
igualmente, son inversamente proporcionales a los cuerpos.”. Aquí Newton,
esencialmente, nos dice que si un cuerpo ejerce fuerza sobre otro, este último
devolverá la acción al primer cuerpo, con la misma intensidad, pero en sentido
contrario.
Información
extraída de Philosophiae naturalis principia mathematica (1687), de
Isaac Newton.
Imagen: Isaac Newton en 1689 por Godfrey Kneller
viernes, 15 de mayo de 2020
Podemos ser matemáticos
Una cosa que tengo más clara que eso de si las matemáticas están implícitas en la naturaleza o son cosa nuestra es que los seres humanos somos matemáticos, esencialmente matemáticos. Para empezar, hay una serie de cuestiones obvias y que compartimos con gran cantidad de otros seres de los que pueblan este planeta: la capacidad para contar, medir, hacer sencillos cálculos... Todo esto viene de muy antiguo, por mecanismos evolutivos que se pierden en la oscuridad de lostiempos. Se ha comprobado que los leones, los lobos y, sobre todo, las hienas son capaces de contar rudimentariamente, o al menos tener en cuenta la cardinalidad (el numero de elementos) de distintos conjuntos de objetos, plantas o animales. Se sabe que algunos de lossimios superiores tambien pueden contar y hacer ciertos cálculos. Es bastante curiosa la investigacion de la neurobióloga Margaret Livignstone, de la Medical School de Harvard. Esta Científica quería comprobar si los macacos Rhesus (que viven por la India y China) podían adquirir habilidades aritméticas, o sea, asociar símbolos a cantidades (nuestros números, por ejemplo). Probó con cantidades desde 0 a 25. Para simbolizar las primeras usó los números que utilizamos nosotros, del 0 al 9, y a partir del 10 usó letras. A continucación les daba a elegir símbolos de éstos, y los macacos elegían el símbolo que correspondia a una cantidad mayor de gotas de agua o de zumo. La cosa fue a más porque les hacia elegir entre una suma o un solo simbolo. Por ejemplo, a un lado ponía 5+7 y al otro 9. En unos cuatro meses los macacos aprendieron a sumar dos números y comparar el resultado con un tercer número. O sea, que llegaban a saber que 5+7 significaba algo mayor que 9. Al parecer, el concepto de número está inscrito de forma muy profunda en nuestro ser. A lo largo de la historia este concepto ha evolucionado hasta tener varios significados diferentes. Cuando decimos número nos podemos estar refiriendo a cosas muy diferentes. ¿Te has preguntado alguna ves qué es un número?. Vale, de momento tenemos claro que tanto los animales como los estadios mas primitivos de nuestro cerebro son capaces de asimilar conceptos numericos y hacer algunos calculos basicos. Son habilidades que podriamos calificar plenamente como matematicas, y que estan en nuestro camino evolutivo.

Pero sin ir mas allá. Sin entrar en grandes profundidades antropológicas, metafísicas, psicológicas o filosóficas. Déjame hablar para el humano medio de nuestros días, que ve la tele, ha ido al colegio, sale con los amigos o le gusta ir al monte. Ese ser humano que alguna vez piensa eso de que "a mi no se me dan bien las mates" o lo ha oido decir. Que tiene a su matemático interior abandonado del todo, pero lo tiene, aunque no sea conciente de ello. ¿Y qué sabe hacer ese matematico que todos tenemos dentro? Todo el mundo, salvo algunas excepciones, posee una capacidad hermosa de razonamiento lógico del mismo modo quetodo el mundo, salvo excepciones puede correr. Y las excepciones no son tantas, porque, al igual que existen ayudas para algunas personas que por sus porpios medios no serian capaces de correr, tambien uno puede buscar apoyos para su razonamiento logico, Esta claro que aunque uno no sea Usain Bolt o Hisham El Gerrouj, todos tenemos la capacidad de correr. La podemos practicar y entrenar o podemos habandonar nuestro cuerpo hasta provocarle una incapacidad que quiza no tendria por que tener, a base de sedentarismo y hamburguesas rellenas de perritos calientes rellenos de queso. Con la capacidad de razonamiento logico pasa lo mismo. El mecanismo lo tenemos, y no hace falta que todos seamos genios matematicos, pero tampoco esta bien que nos abandonemos del todo. ¿Tú has visto la cantidad de runners que corren hoy en día? Es verdad que es como una especie de moda obsesivo-compulsiva, pero tambien lo es que muchos de nuestros corredores aficionados que inundan nuestros parques y calles disfrutan con lo que hacen y van mejorando, cada cual dentro desu nivel. ¿Te imaginas que de repente la gente se aficiona, asá, en masa, a darle al coco? Igual deberiamos ponerle un nombre en ingles como pasa con los runners y el running, y asi a lo mejor la gentese aficionaba más: ejércitos de thinkers, aficionados al thinking mejorando día a día y disfrutando con lo que hacen. Molaría. Y no me parece que la comparacion sea descabellada. Estamos naturalmente preparados para correr, mira a los niños chiquitines. Y estamos naturalmente dotados para el pensamiento lógico (mira a los niños chiquitines). Somos perfectamente capaces de seguir un razonamiento lógico. Y eso se puede entrenar. Hemos llegado a uno de los primeros puntos clave. Créeme, el razonamiento lógico es la base de las matemáticas. El autentico nucleo de las matematicas esta en el razonamiento logico, no en saberse un millos de decimales de π o en ser capaz de dividir numeros de ocho cifras. El centro de las matemáticas es una mezcla de imaginacion, creatividad y razonamiento lógico, y eso se concreta en la argamasa que mantiene en pie el hacer crecer el edificio de las matemáticas: los teoremas y sus demostraciones.

macaco en experimetno de la neurobióloga Margaret Livignstone
Fragmento extraido del libro "Inteligencia Matemática (Eduardo Sáenz Cabezón)"
jueves, 14 de mayo de 2020
El hombre que supo por qué brillan las estrellas
El abril de 1938, dos de los gigantes de la física moderna, el ucraniano Georgi Gamow (1904-1968) y el norteamericano Edward Teller (1908-2003), organizaban un congreso en la Carnegie Institution de Washington. Su objetivo: resolver el problema de por qué brillan las estrellas. Entre los participantes se encontraba un refugiado de la Alemania nazi, experto en procesos nucleares y que daba clases en la universidad de Cornell. Su nombre era Hans Bethe (1906-2005). Pensador efervescente, tenía un talento innato para la física y las matemáticas: parecía que se dedicaba a jugar con números y letras. En la reunión de Washington, los astrónomos dijeron a los físicos todo lo que sabían de la constitución interna de las estrellas, que era mucho, y eso sin conocer realmente cómo se generaba la energía en su interior. Uno de los textos clásicos de la astrofísica, On the Constitution of the Stars, escrito por el brillante Arthur Eddington, describía perfectamente la estructura interna de las estrellas sin necesidad de mencionar nada sobre la naturaleza de su motor energético. Ahora le tocaba a los físicos ponerse a trabajar.
La determinación de Bethe
De vuelta en Cornell, Bethe atacó y resolvió el problema con tanta rapidez que Gamow llegaría a decir que había calculado la respuesta antes de que el tren llegase a la estación de destino. Bethe envió el artículo describiendo su hallazgo a la revista Physical Review, pero entonces uno de sus estudiantes le comentó que la academia de Ciencias de Nueva York ofrecía un premio de 500 dólares al mejor artículo inédito sobre la producción de energía en las estrellas. Bethe pidió a la revista que le devolviese el artículo, lo mandó al concurso y, evidentemente, ganó. El físico tenía sus motivos para hacerlo. Su madre se encontraba todavía en Alemania y aunque los nazis accedían a dejarla salir, pedían 250 dólares si, además, quería llevarse sus muebles. Bethe destinó la mitad del premio para ello. Solamente después permitió que se publicara su artículo, con el que ganó el premio Nobel en 1967.
La determinación de Bethe
De vuelta en Cornell, Bethe atacó y resolvió el problema con tanta rapidez que Gamow llegaría a decir que había calculado la respuesta antes de que el tren llegase a la estación de destino. Bethe envió el artículo describiendo su hallazgo a la revista Physical Review, pero entonces uno de sus estudiantes le comentó que la academia de Ciencias de Nueva York ofrecía un premio de 500 dólares al mejor artículo inédito sobre la producción de energía en las estrellas. Bethe pidió a la revista que le devolviese el artículo, lo mandó al concurso y, evidentemente, ganó. El físico tenía sus motivos para hacerlo. Su madre se encontraba todavía en Alemania y aunque los nazis accedían a dejarla salir, pedían 250 dólares si, además, quería llevarse sus muebles. Bethe destinó la mitad del premio para ello. Solamente después permitió que se publicara su artículo, con el que ganó el premio Nobel en 1967.
En 1938, el físico alemán Hans Bethe
encontró el mecanismo de las reacciones
nucleares que explica cómo las estrellas
producen su energía.
Fragmento sacado el libro "FEYNMAN La electrodinámica cuántica" pag. 72
Colección RBA "GRANDES IDEAS DE LA CIENCIA"
martes, 28 de abril de 2020
La física a partir de Newton
La obra de Isaac Newton representa una de las mayores contribuciones de la ciencia realizadas nunca por una persona. Entre otras cosas, Newton dedujo la ley de la gravitación universal, inventó el cálculo infinitesimal y realizó experimentos para estudiar la naturaleza de la luz y el color.
A partir de 1665, cuando tenía 23 años, Newton desarrolló los principios de la mecánica, formuló la ley de la gravitación universal, separó la luz blanca en sus colores constituyentes e inventó el cálculo diferencial e integral. Las contribuciones de Newton cubrieron una gama muy amplia de fenómenos naturales. Por ejemplo, demostró que tanto las leyes de Kepler sobre el movimiento planetario como los descubrimientos de Galileo sobre la caída de los cuerpos se deducen de la segunda ley del movimiento (segunda ley de Newton) combinada con la ley de la gravitación. Newton también logró explicar el efecto de la luna sobre las mareas, así como la precesión de los equinoccios.
El desarrollo de la mecánica:
El posterior desarrollo de la física se debe mucho a las leyes del movimiento o leyes de Newton, especialmente a la segunda, que afirma que la fuerza necesaria para acelerar un objeto es igual a su masa multiplicada por su aceleración. Si se conoce la posición y velocidad iniciales de un cuerpo, así como la fuerza aplicada, es posible calcular las posiciones y velocidades posteriores aunque la fuerza cambie con el tiempo o la posición; en esos casos es necesario aplicar el cálculo infinitesimal de Newton. La segunda ley del movimiento también contiene otro aspecto importante: todos los cuerpos tienen una propiedad intrínseca, su masa inercial, que influye en su movimiento. Cuanto mayor es esa masa, menor es la aceleración que adquiere cuando se aplica una fuerza determinada sobre el cuerpo. Hoy sabemos que esta ley es válida siempre que el cuerpo no sea extremadamente pequeño, grande o rápido. La tercera ley de Newton, que afirma que “a cada fuerza de acción corresponde una fuerza de reacción igual y opuesta”, podría expresarse en términos modernos como que todas las fuerzas entre partículas se producen en pares de sentido opuesto, aunque no necesariamente situados a lo largo de la línea que une las partículas.

Fragmento del libro “Física, la enciclopedia” pag. 23 Rubiños ediciones (2013)
lunes, 20 de abril de 2020
Los números de Cantor
1845 El 3 de marzo, en San Petersburgo, Rusia, nace Georg Ferdinand Ludwig Philipp Cantor, hijo de Georg Waldemar Cantor y de Maria Arma Bohm.
1856 La familia Cantor se muda a Alemania.
1862 Cantor desea estudiar matemáticas, pero su padre se opone e ingresa en el Politécnico de Zúrich para estudiar ingeniería. Pocos meses después, el padre le da su permiso para que estudie matemáticas, en el mismo centro.
1863 Muere su padre; Georg y su madre se mudan a Berlín, donde completará sus estudios de matemáticas.
1867 Obtiene el doctorado en matemáticas en la Universidad de Berlín.
1869 Comienza a trabajar en la Universidad de Halle.
1872 Conoce a Richard Dedekind. Muchas de las ideas de Cantor sobre el infinito saldrán a la luz por primera vez en cartas escritas a Dedekind.
1874 Se casa con Vally Guttmann; los Cantor tendrán seis hijos. Ese mismo año se publica su artículo «Sobre una propiedad característica de la totalidad de los números reales algebraicos», donde aparecen por primera vez sus ideas sobre el infinito, aunque, por recomendación de Karl Weierstrass, esas ideas están «ocultas».
1878 Se publica «Una contribución a la teoría de las variedades», donde Cantor plantea explícitamente sus ideas sobre el infinito. Leopold Kronecker pone en juego toda su influencia para evitar que el artículo se publique.
1883 Publicación de «Fundamentos para una teoría general de variedades», que constituye el punto culminante de la creatividad matemática de Cantor.
1884 En mayo sufre un ataque depresivo, y abandona toda investigación matemática durante más de cinco años.
1890 Se crea la Unión Matemática Alemana y Cantor es elegido como su primer presidente.
1892 Se publica «Sobre una cuestión elemental de la teoría de las variedades», donde aparece su famosa «demostración de la diagonal».
1895 Publicación de la primera parte de «Contribuciones a la creación de una teoría de los cortjuntos transfinitos»; la segunda parte vio la luz en 1897.
1899 El 16 de diciembre muere su hijo Rudolf, de trece años. La pérdida desencadena en Cantor una enfem1edad mental de la que nunca se recuperó.
1918 Fallece en la clínica psiquiátrica de Halle el 6 de enero.
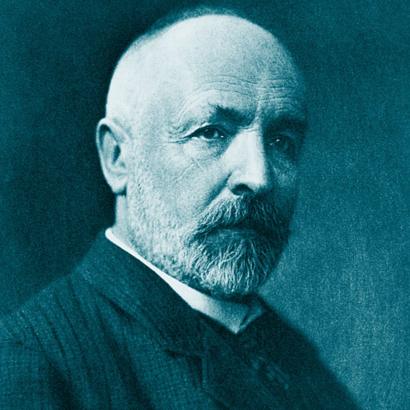
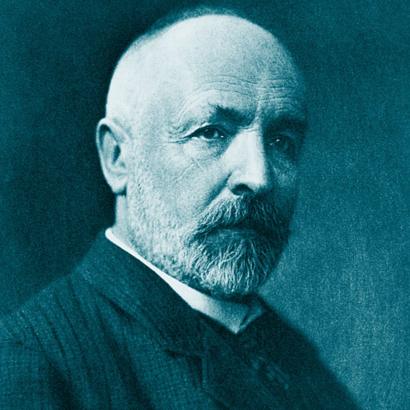
lunes, 13 de abril de 2020
La Leyenda de George Dantzi, El problema matemático irresoluble
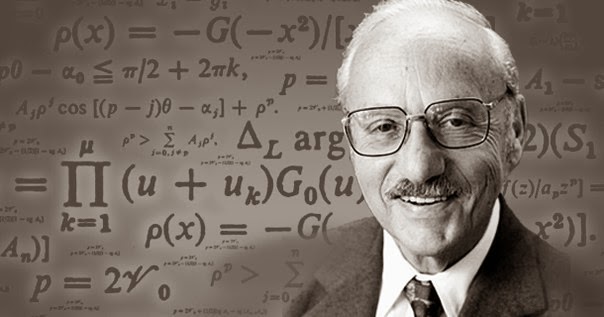
Un joven estudiante universitario estaba trabajando duro en un curso de matemáticas de nivel superior, por temor a no poder aprobar. La noche antes de la final, estudió tanto que durmió la mañana de la prueba.
Cuando corrió al aula varios minutos tarde, encontró tres ecuaciones escritas en la pizarra. Los dos primeros fueron bastante fáciles, pero el tercero parecía imposible. Trabajó frenéticamente en ello hasta que, a solo diez minutos de la fecha límite, encontró un método que funcionó y terminó los problemas justo cuando se le solicitó el tiempo.
El estudiante entregó su examen y se fue. Esa noche recibió una llamada telefónica de su profesor. "¿Te das cuenta de lo que hiciste hoy en el examen?" le gritó al estudiante.
"Oh, no", pensó el estudiante. No debo haber solucionado los problemas después de todo.
"Se suponía que solo debías resolver los dos primeros problemas", explicó el profesor. “Ese último fue un ejemplo de una ecuación que los matemáticos desde Einstein han estado tratando de resolver sin éxito. Lo discutí con la clase antes de comenzar la prueba. ¡Y acabas de resolverlo!
¡Y esta versión en particular es aún más interesante por estar basada en un incidente de la vida real!
Un día, en 1939, George Bernard Dantzig, candidato a doctorado en la Universidad de California, Berkeley, llegó tarde a una clase de estadística de posgrado y encontró dos problemas escritos en la pizarra. Sin saber que eran ejemplos de problemas estadísticos "no resueltos", los confundió con parte de una tarea, los anotó y los resolvió. (Las ecuaciones abordadas por Dantzig se describen con mayor precisión no como problemas irresolubles, sino como teoremas estadísticos no comprobados para los cuales elaboró pruebas).
Seis semanas después, el profesor de estadística de Dantzig le notificó que había preparado una de sus dos pruebas de "tarea" para su publicación, y a Dantzig se le otorgó el crédito de coautor en otro documento varios años más tarde, cuando otro matemático ideó de forma independiente la misma solución para el segundo problema.
George Dantzig relató su hazaña en una entrevista de 1986 para el College Mathematics Journal:
Sucedió porque durante mi primer año en Berkeley llegué tarde un día a una de las clases de [Jerzy] Neyman. En la pizarra había dos problemas que supuse que habían sido asignados para la tarea. Los copié. Unos días después, me disculpé con Neyman por tomar tanto tiempo para hacer la tarea, los problemas parecían ser un poco más difíciles de lo habitual. Le pregunté si todavía lo quería. Me dijo que lo tirara sobre su escritorio. Lo hice de mala gana porque su escritorio estaba cubierto con un montón de papeles que temía que mi tarea se perdiera allí para siempre. Aproximadamente seis semanas después, un domingo por la mañana alrededor de las ocho en punto, [mi esposa] Anne y yo fuimos despertadas por alguien golpeando nuestra puerta. Fue Neyman. Se apresuró con los papeles en la mano, todo emocionado: "Acabo de escribir una introducción a uno de sus papeles. Léalo para que pueda enviarlo de inmediato para su publicación ". Por un minuto no tuve idea de lo que estaba hablando. Para resumir, los problemas en la pizarra que había resuelto pensando que eran tarea eran, de hecho, dos famosos problemas no resueltos en las estadísticas. Ese fue el primer indicio que tuve de que había algo especial en ellos.
Un año después, cuando comencé a preocuparme por un tema de tesis, Neyman se encogió de hombros y me dijo que envolviera los dos problemas en una carpeta y que los aceptaría como mi tesis.
Sin embargo, el segundo de los dos problemas no se publicó hasta después de la Segunda Guerra Mundial. Sucedió de esta manera. Alrededor de 1950 recibí una carta de Abraham Wald que incluía las pruebas finales de galera de un artículo suyo que estaba a punto de imprimir en los Anales de Estadísticas Matemáticas. Alguien acababa de señalarle que el resultado principal en su trabajo era el mismo que el segundo problema de "tarea" resuelto en mi tesis. Le respondí sugiriendo que publiquemos conjuntamente. Simplemente insertó mi nombre como coautor en la prueba de galera.
El Dr. Dantzig también explicó cómo su historia pasó al reino de la leyenda urbana:
El otro día, mientras daba un paseo temprano por la mañana, Don Knuth me saludó mientras pasaba en su bicicleta. Es colega en Stanford. Se detuvo y dijo: "Hola, George. Estuve de visita en Indiana recientemente y escuché un sermón sobre ti en la iglesia. ¿Sabes que eres una influencia para los cristianos de América media? Lo miré asombrado. "Después del sermón", continuó, "el ministro se acercó y me preguntó si conocía a un George Dantzig en Stanford, porque ese era el nombre de la persona de quien se trataba su sermón".
El origen del sermón de ese ministro se remonta a otro ministro luterano, el reverendo Schuler [sic] de la Catedral de Cristal en Los Ángeles. Me contó sus ideas sobre pensar positivamente, y le conté mi historia sobre los problemas de tarea y mi tesis. Unos meses más tarde recibí una carta de él pidiéndome permiso para incluir mi historia en un libro que estaba escribiendo sobre el poder del pensamiento positivo. La versión publicada de Schuler era un poco confusa y exagerada, pero esencialmente correcta. La moraleja de su sermón era la siguiente: si hubiera sabido que el problema no era la tarea, sino que en realidad eran dos problemas famosos no resueltos en estadística, probablemente no habría pensado positivamente, me habría desanimado y nunca los habría resuelto.
La versión de la historia de Dantzig publicada por el televangelista cristiano Robert Schuller contenía una gran cantidad de adornos y desinformación que desde entonces se ha propagado en formas de cuentos urbanos como la leyenda, como el citado al principio de esta página: Schuller convirtió la tarea equivocada Asignación a un "examen final" con diez problemas (ocho de los cuales eran reales y dos de los cuales eran "irresolubles"), afirmó que "incluso Einstein no pudo descubrir los secretos" de los dos problemas adicionales, y declaró erróneamente que el profesor de Dantzig quedó tan impresionado que "le dio a Dantzig un trabajo como asistente, y Dantzig ha estado en Stanford desde entonces".
George Dantzig (él mismo, hijo de un matemático) recibió una licenciatura de la Universidad de Maryland en 1936 y una maestría de la Universidad de Michigan en 1937 antes de completar su Doctorado (interrumpido por la Segunda Guerra Mundial) en UC Berkeley en 1946. Más tarde trabajó para la Fuerza Aérea, tomó un puesto con la RAND Corporation como matemático de investigación en 1952, se convirtió en profesor de investigación de operaciones en Berkeley en 1960, y se unió a la facultad de la Universidad de Stanford en 1966, donde enseñó y publicó como profesor de investigación de operaciones. hasta la década de 1990. En 1975, el Dr. Gerald Ford le otorgó al Dr. Dantzig la Medalla Nacional de la Ciencia.
George Dantzig falleció en su casa de Stanford a los 90 años el 13 de mayo de 2005.
Referencias:
Stanford Celebra el cumpleaños número 80 de Dantzig.
Entrevista a George Bernard Dantzig publicada en The College Mathematical Journal, en marzo de 1986.
Obituario de George Dantzig.
viernes, 10 de abril de 2020
La NASA conmemora el 50 aniversario del Apolo 13, 'Un fracaso exitoso'
Mientras la NASA celebra el 50 aniversario de la misión Apolo 13 , que se conoce como "un fracaso exitoso" , la agencia comparte una variedad de recursos, reconociendo el triunfo de el equipo de control de la misión y los astronautas, y observando cómo esas lecciones aprendidas se pueden aplicar a su programa lunar Artemis.
"Nuestro objetivo hace 50 años era salvar a nuestra valiente tripulación después de enviarlos alrededor de la Luna y devolverlos a salvo a la Tierra", dijo el administrador de la NASA Jim Bridenstine. “Nuestro objetivo ahora es regresar a la Luna para quedarnos de manera sostenible. Estamos trabajando arduamente para asegurarnos de que no necesitamos responder a este tipo de emergencia en Artemis, sino de estar preparados para responder a cualquier problema que no prevemos ”.
La tripulación del Apolo 13 estaba compuesta por el comandante James (Jim) Lovell Jr., el piloto del módulo de comando John Swigert Jr. y el piloto del módulo lunar Fred Haise Jr. Su cohete Saturno V se lanzó a las 2:13 pm EST del 11 de abril de 1970, desde el lanzamiento Pad 39A en el Centro Espacial Kennedy de la NASA en Florida. El módulo de comando se llamaba Odyssey, y el módulo lunar se llamaba Acuario.
Mientras se dirigía a la Luna el 13 de abril, se rompió un tanque de oxígeno en el módulo de servicio Apollo. El aterrizaje lunar y los paseos lunares, que hubieran sido ejecutados por Lovell y Haise, fueron abortados cuando un equipo dedicado de controladores de vuelo y expertos en ingeniería en el Centro de Control de la Misión Apollo dedicaron sus esfuerzos a desarrollar un plan para albergar a la tripulación en el módulo lunar. un "bote salvavidas" y retener los recursos suficientes para llevar la nave espacial y su tripulación a casa de forma segura. La caída se produjo en el Océano Pacífico a la 1:07 pm del 17 de abril, luego de un vuelo que duró cinco días, 22 horas y 54 minutos.

Insignnia Apollo 13
Referencias:
Suscribirse a:
Comentarios (Atom)




