El Pensamiento Físico-Matemático es en sí mismo la representación visible de la muy conocida pero poco comprendida, relación entre la Física y las Matemáticas, que ubica a la matemática como el lenguaje ó la herramienta que permite caracterizar los distintos fenómenos físicos por medio del uso de algoritmos. Muchas personas se han preguntado sobre la diferencia de estos, y en este caso fue una historia de una de las mentes mas brillandes habidas en la humanidad, la que da un claro ejemplo en el desarrollo de estos pensamientos, John von Neumann quien fue un matemático húngaro-estadounidense conocido por realizar contribuciones fundamentales en física cuántica, análisis funcional, teoría de conjuntos, teoría de juegos, ciencias de la computación, economía, análisis numérico, cibernética, hidrodinámica, estadística y muchos otros campos, un dia en una conversacion casual con un interlocutor que habia estudiado aspectos sobre aprendizaje en matematicas, le comenta un roblema: Dos trenes están en la misma vía, a una distancia de 100 km, uno hacia el otro, cada uno a una velocidad de 50 km/h. Una mosca que comienza en la parte delantera de un tren vuela hacia el otro a una velocidad de 75 km/h. Al llegar al otro tren, la mosca se da vuelta y continúa hacia el primer tren. ¿Cuántos kilómetros recorre la mosca antes de ser aplastada en la colisión de los dos trenes?.
Von Neumann casi inmediatamente respondio "75 km".
El interlocutor dijo: "Correcto. Pero ahora sé, por la rapidez de su respuesta, que usted es realmente un físico, no un matemático. El matemático habría calculado que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora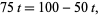 
o 
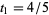, en qué punto ha recorrido una distancia 
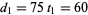km. Luego se da vuelta y llega al primer tren nuevamente cuand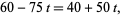o 
o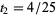 
continuando, la distancia total recorrida por la mosca se obtiene sumando la serie 
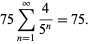. Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.
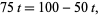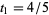o , en qué punto ha recorrido una distancia 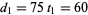km. Luego se da vuelta y llega al primer tren nuevamente cuand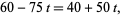o o 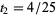continuando, la distancia total recorrida por la mosca se obtiene sumando la serie 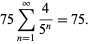. Pero un físico habría tomado un atajo; los físicos se habrían dado cuenta de que los trenes tardan una hora en colisionar (su velocidad relativa es de 100 km/h y inicialmente están separados por 100 km). Dado que la mosca viaja a 75 km/h y vuela continuamente hasta que se aplasta (lo que se supone que ocurre una fracción de segundo antes de que los dos trenes que se aproximan se aplastan entre sí), por lo tanto, debe viajar 75 km en el tiempo de la hora.Von Neumann: "¡Oh, esa es una forma inteligente de resolverlo! Pero yo sumé la serie".
John Von Neumann
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 42, 2003.
No hay comentarios.:
Publicar un comentario